Power and Amplitude: Watts, Volts and Referenced Decibels

Introduction
In radio frequency applications (but also in a lot of other application) is very common to deal with very large and very small signals. For example, a transceiver may transmit a power of 100 W and receive only 10 fW (or 0.000'000'000'000'01 W). These extremely different power levels may share the same circuits. Of course, these figures can be expressed in Watts using the engineering notation (as above) or with the scientific notation, like 1·102 W and 1·10–14 W, but they are quite difficult to pronounce and if the exponent is misspelled, the resulting error will be huge.

Another way is to take the logarithm and convert all the powers in dBm. 100 W become +50 dBm and 10 fW become –110 dBm: these figures are much easier to handle by heart and to write. Then, if attenuation and gain of different circuit blocks are also expressed in dB, to find the final power, one can simply add everything together instead of multiplying, further simplifying calculations.

Not everybody is comfortable with dB, dBm and similar (pseudo) units: there is no strict need to use them, but they are so widely used in engineering that is very difficult to avoid them.

Some theory
Decibels (dB) are used to express power ratios in a logarithmic way, so that very large and very small powers can be compared using comfortable numbers. A decibel is a dimensionless pseudo-unit because it's defined by the ratio of two powers. But since decibels are so handy, to express true power instead of just a dimensionless ratio, referenced decibels are very often used.

If we talk about power, the following equation defines the power level P in dB of the power p in W referenced to the power p0:

The 10 factor is because decibels are "tenth of Bells". But I never heard of any measurement done in Bells, only decibels are used.

The most common unit is the dBm (pronounce "d-B-m") also known as dBmW or decibel-milliwatt: it's just the power level in dB compared to a reference power of p0 = 1 mW. Sometimes also dBW are used and they express the power ratio relative to p0 = 1 W, but they are not very common.

As shown in the above plot, the logarithmic effect of the decibel conversion is quite evident. As one can see on this log-lin plot, dBm and dBW are just two straight lines separated by 30 dB: to convert dBm into dBW simply subtract 30.

In some domains, like analog TV reception, it's common to measure voltage instead of power. This is not a problem as long as the impedance is known and fixed (TV receivers usually use 75 Ω).

Absolute voltages can also take advantage of the decibel logarithmic scale by using decibel-microvolt (dBμV) and decibel-volts (dBV). The most common is the dBμV which express the voltage ratio relative to u0 = 1 μV. Sometimes dBV are also used and they express the voltage ratio relative to u0 = 1 V.

Beware that voltages use a "20" instead of a "10" in their dB formula. This is because decibels are always defined as power rations; if we only have voltages, we have to square them first to find the power. That power of two, when taken out of the logarithm will multiply the existing factor of 10 by 2.

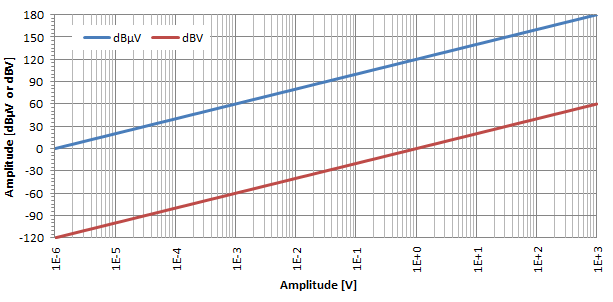
As shown in the above plot and in a similar way as before, the logarithmic effect of the decibel conversion is quite evident also for voltages. As one can see on this log-lin plot, dBμV and dBV are just two straight lines separated by 120 dB: to convert dBμV into dBV simply subtract 120.

Now, if we want to convert from power to voltage and vice versa, we need to know the impedance. We just use the following equation:

This conversion is only valid when the impedance Zc is real and the load is matched to the transmission line.

If we plot the power level in dBm and the amplitude level in dBμV as a function of power in W for a given impedance (here Zc = 50 Ω) we get the following:

As before, we have two parallel lines 107 dB apart. So, to convert from dBm to dBμV, simply add 107 dB for Zc = 50 Ω, add 109 dB for Zc = 75 Ω, add 115 dB for Zc = 300 Ω or add 118 dB for Zc = 600 Ω.

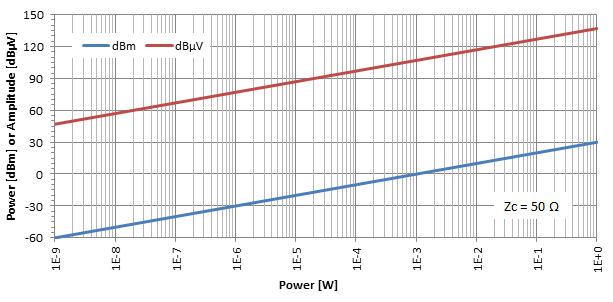
Practical considerations
At first glance, one may think that because of the logarithm, a pocket calculator is absolutely necessary to deal with dBm. Actually, a rough calculation can easily be done in your head. You have to remember just three facts:
 A power of 1 mW is 0 dBm.
 Every time the power doubles, add 3 dB.
 Every time the power increases by a factor of 10, add 10 dB.

Now, let's consider a few examples: suppose we have a power level of 26 dBm. We can write 26 dBm = 0 dBm + 10 dB + 10 dB + 3 dB + 3 dB, and with the previous three simples rules, we can easily find the power by doing 1 mW · 10 · 10 · 2 · 2 = 400 mW.

Another example: suppose we have –33dBm: we can write as –33 dBm = 0 dBm – 10 dB – 10 dB – 10dB – 3 dB, and we find 1 mW / 10 / 10 / 10 / 2 = 0.5 μW.

This works also in the in other way around, for example 50 mW are just 1 mW · 10 · 10 / 2. In dBm we have 0 dBm + 10 dB + 10 dB –3 dB = 17 dBm.

This requires some practice but is very easy to do. It's not as accurate as a pocket calculator because you can only be accurate at ±2 dB but, for the effort, gives a very good idea of the strength of a signal.

A similar method also works for dBμV, but the rules are different:
 An amplitude of 1 μV is 0 dBμV.
 Every time the amplitude doubles, add 6 dB.
 Every time the amplitude increases by a factor of 10, add 20 dB.

You may be surprised about the calculations in decibels shown before, where dB are added to dBm, which is quite strange. This is because decibels are pseudo-units and do not behave as usual. The ratio of two powers is expressed in dB but is dimensionless: for example 3 dB only means "twice as much". The power expressed in dBm is really a power: for example 10 dBm means "10 times stronger than 1 mW", which is 10 mW.

Now, when you add decibels (dB, dBm,...), because of their logarithmic nature, you are actually multiplying the original figures together. So, if you add a gain of 3 dB to a power of 10 dBm, you obtain 13 dBm. But what you really did, is multiplying a factor of 2 with a power of 10 mW obtaining 20 mW, which is 13 dBm!

So far so good, adding is much easier to do in your head than multiplying, and this makes decibels so handy. But there is a problem: since adding decibels together correspond to multiplying the original factors, how can one add (combine) the power of two signals? Well, you can't. You can't add dBm to dBm. If, for example, you have a circuit or a device that combines the power of one signal of 10 dBm (10 mW) with the power of another signal of 13 dBm (20 mW), the result is 10 mW + 20 mW = 30 mW which is 14.8 dBm. There is no way of doing this directly in dBm, you have to convert both powers in Watts, add them together and convert them back in dBm. This is a big limitation of decibels and a common pitfall; fortunately this operation is not very common.

If you would like to build a radio station, boost your FM radio transmitter or need any other FM equipment, please feel free to contact us: [email protected].

Leave a message 

Message List