Products Category
- FM Transmitter
- 0-50w 50w-1000w 2kw-10kw 10kw+
- TV Transmitter
- 0-50w 50-1kw 2kw-10kw
- FM Antenna
- TV Antenna
- Antenna Accessory
- Cable Connector Power Splitter Dummy Load
- RF Transistor
- Power Supply
- Audio Equipments
- DTV Front End Equipment
- Link System
- STL system Microwave Link system
- FM Radio
- Power Meter
- Other Products
- Special for Coronavirus
Products Tags
Fmuser Sites
- es.fmuser.net
- it.fmuser.net
- fr.fmuser.net
- de.fmuser.net
- af.fmuser.net ->Afrikaans
- sq.fmuser.net ->Albanian
- ar.fmuser.net ->Arabic
- hy.fmuser.net ->Armenian
- az.fmuser.net ->Azerbaijani
- eu.fmuser.net ->Basque
- be.fmuser.net ->Belarusian
- bg.fmuser.net ->Bulgarian
- ca.fmuser.net ->Catalan
- zh-CN.fmuser.net ->Chinese (Simplified)
- zh-TW.fmuser.net ->Chinese (Traditional)
- hr.fmuser.net ->Croatian
- cs.fmuser.net ->Czech
- da.fmuser.net ->Danish
- nl.fmuser.net ->Dutch
- et.fmuser.net ->Estonian
- tl.fmuser.net ->Filipino
- fi.fmuser.net ->Finnish
- fr.fmuser.net ->French
- gl.fmuser.net ->Galician
- ka.fmuser.net ->Georgian
- de.fmuser.net ->German
- el.fmuser.net ->Greek
- ht.fmuser.net ->Haitian Creole
- iw.fmuser.net ->Hebrew
- hi.fmuser.net ->Hindi
- hu.fmuser.net ->Hungarian
- is.fmuser.net ->Icelandic
- id.fmuser.net ->Indonesian
- ga.fmuser.net ->Irish
- it.fmuser.net ->Italian
- ja.fmuser.net ->Japanese
- ko.fmuser.net ->Korean
- lv.fmuser.net ->Latvian
- lt.fmuser.net ->Lithuanian
- mk.fmuser.net ->Macedonian
- ms.fmuser.net ->Malay
- mt.fmuser.net ->Maltese
- no.fmuser.net ->Norwegian
- fa.fmuser.net ->Persian
- pl.fmuser.net ->Polish
- pt.fmuser.net ->Portuguese
- ro.fmuser.net ->Romanian
- ru.fmuser.net ->Russian
- sr.fmuser.net ->Serbian
- sk.fmuser.net ->Slovak
- sl.fmuser.net ->Slovenian
- es.fmuser.net ->Spanish
- sw.fmuser.net ->Swahili
- sv.fmuser.net ->Swedish
- th.fmuser.net ->Thai
- tr.fmuser.net ->Turkish
- uk.fmuser.net ->Ukrainian
- ur.fmuser.net ->Urdu
- vi.fmuser.net ->Vietnamese
- cy.fmuser.net ->Welsh
- yi.fmuser.net ->Yiddish
Quadrature Frequency and Phase Demodulation
Radio Frequency Demodulation
This page explores the use of quadrature demodulation with frequency- and phase-modulated signals.
From the previous page we know that quadrature demodulation produces two baseband waveforms that, when taken together, convey the information that was encoded into the carrier of the received signal.
More specifically, these I and Q waveforms are equivalent to the real and imaginary parts of a complex number.
The baseband waveform contained in the modulated signal corresponds to a magnitude-plus-phase representation of the original data, and quadrature demodulation converts that magnitude-plus-phase representation into I and Q signals that correspond to a Cartesian representation.

It is perhaps not very surprising that we can use quadrature demodulation to demodulate AM signals, considering that a quadrature demodulator is simply two amplitude demodulators driven by carrier-frequency reference signals that have a 90° phase difference.
However, one of the most important characteristics of quadrature demodulation is its universality. It works not only with amplitude modulation but also with frequency and phase modulation.
Quadrature Frequency Demodulation
First let’s look at the I and Q waveforms that are produced when we apply quadrature demodulation to frequency modulation. The received FM waveform is a 100 kHz carrier modulated by a 100 Hz sinusoid.
We’re using the same quadrature demodulator that was used in the AM simulation; it has two arbitrary behavioral voltage sources for performing the multiplication, and each voltage source is followed by a two-pole low-pass filter (the cutoff frequency is ~1 kHz).
You can refer to the page on How to Demodulate an FM Waveform for information on how to create an FM signal in LTspice.

Perhaps the common reaction to this plot would be confusion. What do these odd-looking signals have to do with the constant-frequency sinusoid that should result from the demodulation process? First let’s make two observations:
*Clearly, the frequency of the I and Q signals is not constant. You may find this a bit confusing at first, since we know that I/Q modulation involves the amplitude modulation of quadrature carriers. Why is the frequency changing as well? It’s essential to remember that these I/Q signals correspond to the modulating signals, not to the quadrature sinusoids that would be added together in a quadrature modulator. The frequency of the modulated quadrature carriers does not change, but the baseband waveforms that serve as the amplitude-modulating signals do not necessarily have constant frequency.
*Though we cannot intuitively interpret the information in this plot, we can see that the signals exhibit periodic variations and that these variations correspond to the period (=10 ms) of the 100 Hz baseband signal.
Finding the Angle
Now that we have I/Q signals, we need to somehow process them into a normal demodulated waveform. Let’s first try the approach that we used with amplitude modulation: use a bit of math to extract the magnitude data.

Clearly this didn’t work: the magnitude signal (the red trace) doesn’t look like a sinusoid, and the frequency is incorrect (200 Hz instead of 100 Hz). After further consideration, though, this is not surprising.
The original data is characterized by magnitude and phase; when we apply the √(I2 + Q2) computation, we are extracting the magnitude. The trouble is, the original data was not encoded in the magnitude of the carrier—it was encoded in the angle (remember that frequency modulation and phase modulation are two forms of angle modulation).
So let’s try a different computation. Let’s extract the angle of the I/Q data rather than the magnitude. As shown in the right-triangle diagram above, we can do this by applying the following equation:
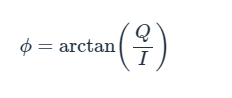
Here is the result:

This doesn’t look good, but we are actually getting close. The red trace represents the instantaneous phase of the original data. (Note that the trace seems more erratic than it really is because the angle is jumping from –90° to +90°, or vice versa).
Frequency modulation, though based on phase, does not encode information directly in the phase of the carrier. Rather, it encodes information in the instantaneous frequency of the carrier, and instantaneous frequency is the derivative of instantaneous phase. So what happens if we take the derivative of the red trace?

As you can see, we have now recovered a waveform that is sinusoidal and has the same frequency as the original baseband signal.
How to Design an Arctangent Circuit
At this point you might be wondering why anyone would want to bother with I/Q demodulation. How in the world would anyone design a circuit that generates an output signal corresponding to the derivative of the arctangent of two input signals?
Well, to answer the question posed in the title of this section, you digitize the signals and compute the arctangent in firmware or software. And this brings us to an important point: Quadrature demodulation is especially advantageous in the context of software-defined radios.
A software-defined radio (SDR) is a wireless communication system in which significant portions of the transmitter and/or receiver functionality are implemented via software. Quadrature demodulation is highly versatile and enables a single receiver to almost instantaneously adapt to different types of modulation.
The I/Q output signals, however, are far less straightforward than a normal baseband signal produced by standard demodulator topologies. This is why a quadrature demodulator and a digital signal processor form such a high-performance receiver system: the digital signal processor can readily apply complicated mathematical operations to the I/Q data produced by the demodulator.
Quadrature Phase Demodulation
The same general considerations that we discussed in the context of quadrature frequency demodulation apply also to quadrature phase demodulation. However, to recover the original data we take the arctangent of (Q/I) rather than the derivative of the arctangent of (Q/I), because the baseband signal is encoded directly in the carrier’s phase rather than in the derivative of the phase (i.e., the frequency).
The following plot was generated by applying quadrature demodulation to a phase-shift-keying waveform consisting of a 100 kHz carrier and a 100 Hz digital baseband signal that causes the carrier’s phase to change by 180° according to whether the signal is logic high or logic low. As you can see, the red trace (whose value corresponds to the phase of the received waveform) reproduces the logic transitions in the baseband signal.

Notice that the red trace is computed via the “atan2” function. Standard arctangent is limited to two quadrants (i.e., 180°) of the Cartesian plane. The atan2 function looks at the individual polarities of the input values in order to produce angles covering all four quadrants.
Summary
*Quadrature demodulation can extract angle information that is relevant to both frequency modulation and phase modulation.
*Radio systems can use a digital signal processor (in conjunction with an analog-to-digital converter) to apply mathematical analysis to I/Q waveforms.
*Baseband phase can be obtained by taking the arctangent of the ratio of Q to I; an “atan2” function is needed if the system must be able to reproduce the full 360° of phase.
*Baseband frequency can be obtained by taking the derivative of the arctangent of the ratio of Q to I.

